原题:对于平面直角坐标系x0y中的线段PQ和点R,给出如下定义:若PR=PQ,则称点R为线段PQ的“P-等长点”。
如图1,已知点A(1,0),B(0,2)。
(1)在点R1(2,0),R2(-1,0), R3(1,-1)中,线段AO的“A-等长点”为:____。
(2)若直线y=x+b上存在线段BO的“B-等长点”,求b的取值范围。
(3)连接AB,
(3.1)若第一象限内的点R是线段BA的“B-等长点”,且△ABR是直角三角形,则点R的坐标为:____。
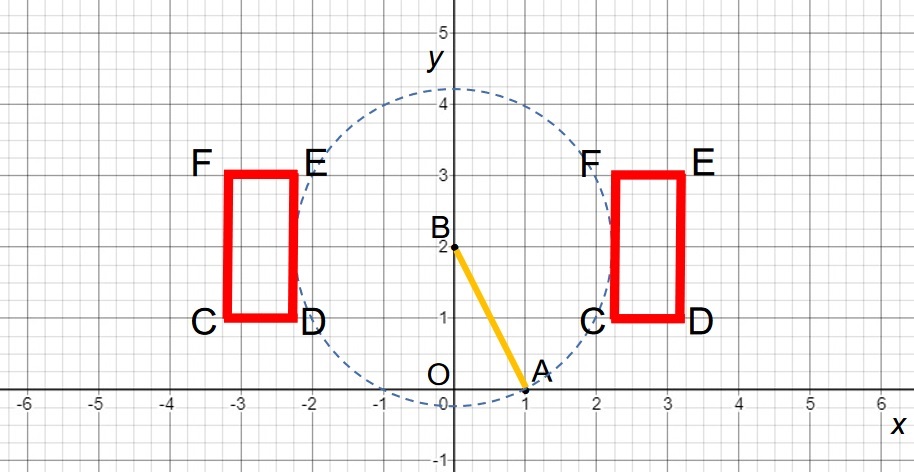
(3.2)矩形CDEF中,DE=2,C(t, 1),D(t+1, 1),若矩形CDEF上存在线段BA的“B-等长点”,结合图象,写出t的取值范围。
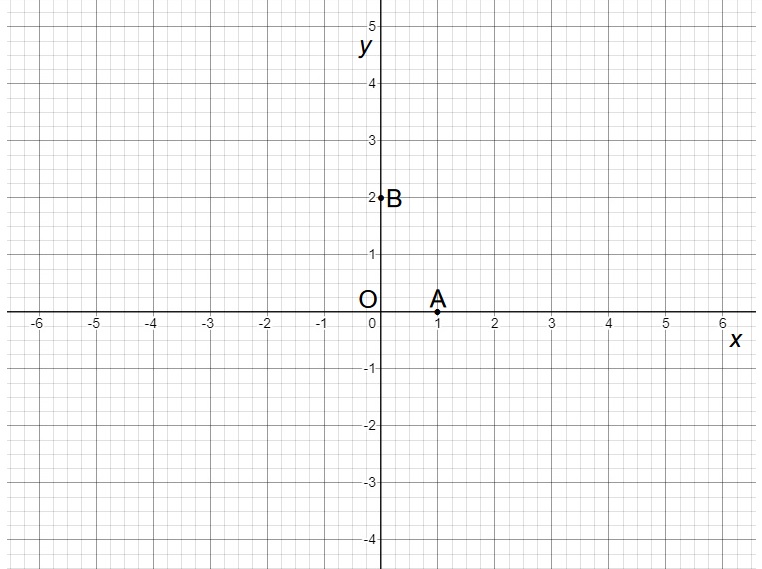
(图1)
解答:
(1)R1,R3。(注:这个题很简单,在图象上画出R1,R2,R3,就能看出答案。AO=AR1=AR3=1)
(2)解题思路:线段BO的B-等长点,必定是落在下图的圆圈之上(因为该圆的半径为2)。通过观察可知,直线y=x+b可以是任意一条45度角的直线。若该直线上存在B-等长点,则该直线必须和圆圈相交或相切。也就是说,直线y=x+b必定是位于下图的两条蓝色直线之间(或与之重合)。继续观察可知,直线y=x+b与y轴的交点,就是b的值。所以,下图中E点到D点,就是b的取值范围。
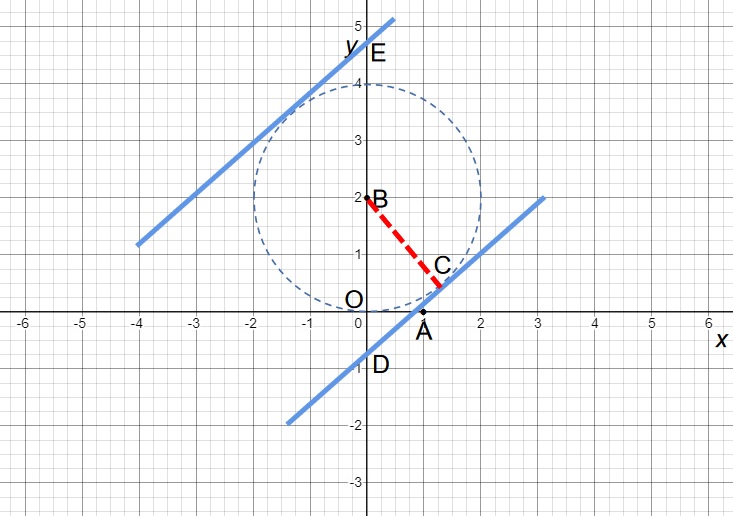
由于角BCD是等腰直角三角形,且BC=CD=2,因此BD^2=BC^2+CD^2,可知BD=√8=2√2。则D点的值为:2-2√2。同理,E点的值为:2+2√2。所以,2-2√2≤b≤2+2√2。
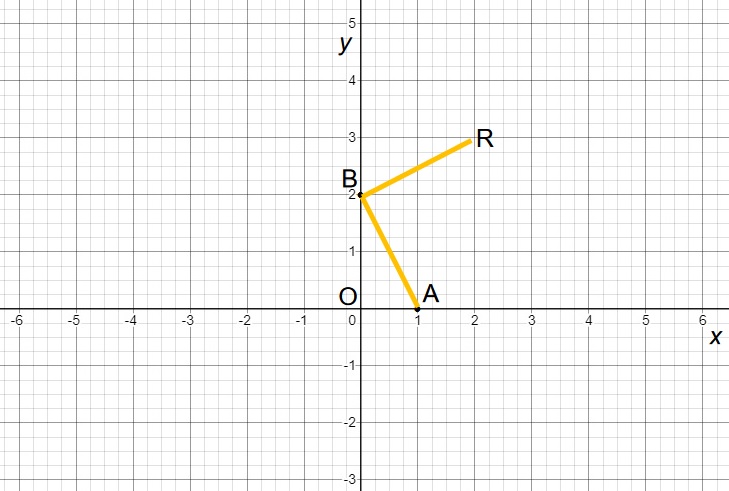
(3.1)如下图,R位于第一象限,且角ABR是直角三角形,则相当于将线段AB逆时针旋转了90度(也可看做是将角ABO逆时针旋转90度),则从图上观察可知,点R的坐标为:(2,3)。
(3.2)从下图观察可知,矩形CDEF可以位于Y轴的左侧和右侧。当位于右侧时,t值最大为:√5。当位于Y轴左侧时,t值最小为:-√5-1。因此,-√5-1≤t≤√5。